Survival analysis -- Theory
生存分析(Survival analysis)是研究影响因素与生存时间和结局关系的方法。简单的说就是要分析影响因素是否与结局相关,还要分析影响因素与结局出现时间关系。
生存分析相关概念
生存时间(Survival time): 指从某起点事件开始到被观测对象出现终点事件所经历的时间,如从疾病确诊到进展/死亡的时间;生存时间有两种类型:
- 完全数据(Complete data),指被观测对象从观察起点到出现终点事件所经历的时间;
- 截尾数据(Censored data),或删失数据,指在出现终点事件前,被观测对象的观测过程终止了。截尾数据的产生主要有三个原因,失访(Loss of follow-up)、退出和终止。失访和退出都是在试验还没有结束时,研究者就已经追踪不到数据了,而终止是研究已经结束仍未观察到患者结局。截尾数据过多会影响生存分析的效果。
死亡概率(Mortality probability) 是指某段时间开始时生存的个体在该段时间内死亡的可能性大小
死亡概率 = 某人群某段时间总死亡例数 / 该人群同时间段期初观察例数
生存概率(Survival probability):是指某段时间开始时存活的个人至该时间结束时仍然存活的可能性大小
生存概率 = 1 - 死亡概率 = 某人群活过某段时间例数 / 该人群同时间段期初观察例数
生存函数(Survival distribution function): 又叫累积生存率,S(t)=P(T>t) ,其中T为生存时间,该函数的意义是生存时间大于时间点t的概率。t=0时S(t)=1,随着t的增加S(t)递减(严格的说是不增),1-S(t)为累积分布函数,表示生存时间T不超过t的概率。
累积生存概率:生存率为多个时间段生存概率的累积,故又称累积生存概率.
生存分析方法
-
非参数法
根据样本的顺序统计量对生存率进行估计,常用的方法有log-rank检验、似然比检验,对于两个及多个生存率的比较,其零假设为两组或多组总体生存时间分布相同,而不对其具体的分布形式及参数进行推断。
常用于随访资料医学研究。- 寿命表(Life Table)
- Kaplan-Meier曲线(乘积极限法Product limit method)
- 分层比较
- 累积风险率
-
半参数法(COX回归)
只规定了影响因素和生存状况间的关系,但是没对时间(和风险函数)的分布情况加以限定。
这种方法主要用于分析生存率的影响因素,属于多因素分析方法,其典型方法是cox比例风险模型。- 模型拟合
- 模型诊断(Model diagnostics)
- 预测风险(Predicted hazard ratios
-
参数法(Parametric proportional hazards models)
参数方法要求观察的生存时间服从某一特定的分布,采用估计分布中参数的方法获得生存率的估计值。生存时间的分布可能为指数分布、weibull分布、对数正态回归分布等,这些分布曲线都有相应的生存率函数形式,只需求得相应参数的估计值,即可获得生存率的估计值和生存曲线。
早期应用于武器使用寿命的研究等。
- 假定生存时间符合weibull分布
- AFT参数转换为Cox模型的β
- 模型比较
- 生存曲线估计
Kaplan-Meier曲线
Kaplan-Meier曲线也称生存曲线, 纵轴表示生存概率,横轴表示生存事件,它是一条下降的曲线,下降的坡度越陡,表示生存率越低或生存时间越短,其斜率表示死亡速率。如果在概率50%处画一条水平线,它将中位生存事件点和生存曲线相交。
Cox 回归 (因素分析)
多数生存时间的分布并不符合指数分布、weibull分布等,不宜采用参数法进行分析。COX回归用于研究各种因素(称为协变量)对于生存期长短的关系,Cox 回归是一种半参数模型,只规定了影响因素和生存时间的关系,但是没有对生存时间的分布情况加以限定。Cox模型分析法以风险率函数作为应变量,以与生存时间可能有关的协变量或交互项作为自变量来分析生存率。与参数模型相比,该模型不能给出各时点的风险率,但可估计出各研究因素对风险率的影响,进行多因素分析。 风险函数(Hazard Function),用h(t)表示,其定义为:
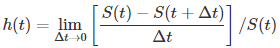
表示时刻t上一个事件瞬时发生的概率,即一个到t时刻存活的个体,在t时刻事件的瞬时发生率。
Cox模型为 lnh(t) = lnh0(t) + β1X1 + ⋯ + βpXp
- X1 + ⋯ + Xp是协变量,β1 + ⋯ + βp是回归系数,由样本估计而得。
- βi>=0表示该协变量是危险因素,越大使生存时间越短
- βi<0表示该协变量是保护因素,越大使生存时间越长
- h0(t)为基础风险函数,它是全部协变量都为0或标准状态下的风险函数,一般是未知的
- h(t)表示当各协变量值X固定时的风险函数,它和h0(t)成比例,所以该模型称为比例风险模型(proportional hazard model)
