变量筛选
在高维数据领域里,变量筛选占据至关重要的地位,有效的变量筛选方法可以从大量的预测变量中剔除多余的变量,挑选出最优子集,从而得到尽可能简洁的模型来提高模型的解释性和预测精度。
模型拟合
当我们进行模型拟合的时候,我们需要衡量一个过度拟合和拟合不足的问题。为了防止过度拟合的一个有效的方法就是对模型的复杂度进行控制。模型的自变量个数越多说明复杂度越高。
约束自变量个数的方法:
- 子集选择:通过逐步回归和最优子集法,对可能的子集进行拟合模型,利用判别准则(如AIC、BIC、Cp、调整R^2^)决定最优模型。问题在于:高维数据计算量大,不稳定。
- 维数约减:主成分回归,把p个变量投影到m维空间(m<p),利用投影得到的不相关组合建立线性模型。问题在于:不能进行变量选择。
- 正则化(基于惩罚):Ridge回归和LASSO回归,通过对最小二乘估计加入罚约束,使某些系数进行压缩,甚至压缩为0,从而实现避免过拟合和变量选择。
LASSO regression
Tibshirani(1996) 提出了Lasso(The Least Absolute Shrinkage and Selectionator Operator)算法。这种算法通过构造一个惩罚函数获得一个精炼的模型;通过最终确定一些指标的系数为零,LASSO算法实现了指标集合精简的目的。这是一种处理具有复共线性数据的有偏估计。Lasso的基本思想是在回归系数的绝对值之和小于一个常数的约束条件下,使残差平方和最小化,从而能够产生某些严格等于0的回归系数,得到解释力较强的模型。
LASSO回归的特点是在拟合广义线性模型的同时进行变量筛选(Variable Selection)和复杂度调整(Regularization)。 因此,不论目标因变量(dependent/response varaible)是连续的(continuous),还是二元或者多元离散的(discrete), 都可以用LASSO回归建模然后预测。 这里的变量筛选是指不把所有的变量都放入模型中进行拟合,而是有选择的把变量放入模型从而得到更好的性能参数。 复杂度调整是指通过一系列参数控制模型的复杂度,从而避免Overfitting。 对于线性模型来说,复杂度与模型的变量数有直接关系,变量数越多,模型复杂度就越高。 更多的变量在拟合时往往可以给出一个看似更好的模型,但是同时也面临过度拟合的危险。 此时如果用全新的数据去验证模型(Validation),通常效果很差。 一般来说,变量数大于数据点数量很多,或者某一个离散变量有太多独特值时,都有可能过度拟合。
LASSO vs. Ridge regression
由于惩罚项的不同而产生了截然不同的岭回归和LASSO回归(岭回归惩罚函数是L2范数, LASSO回归惩罚函数是L1范数)。
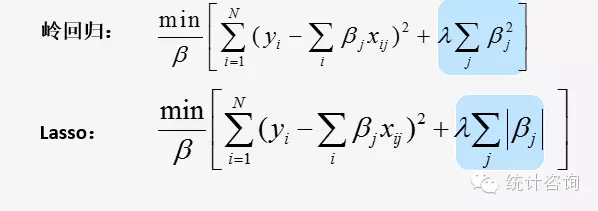
岭回归的惩罚项可以收缩自变量的系数接近0,但并非恰是0(已有算法能收缩到0),保留了原来的自变量个数。这个特点对于模型精度,模型评价影响不大,但给模型解释带来了困难。大牛们都青睐LASSO的原因在于其解决了2个问题:
-
特征选择(Feature Selection):它能实现特征的自动选择,它会学习地去掉这些没有信息的特征,也就是把这些特征对应的权重精准地置为0。
-
可解释性(Interpretability):模型更容易解释;存在大量的自变量的时候,能找出重要的几个自变量,这些变量提供的信息是模型中最重要的。
Elastic Net regression
一般线性Elastic Net模型的目标函数如下:
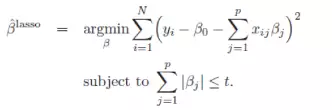
目标函数的第一行与传统线性回归模型完全相同,即我们希望得到相应的自变量系数β,以此最小化实际因变量y与预测应变量βx之间的误差平方和。 而线性Elastic Net与线性回归的不同之处就在于有无第二行的这个约束,线性Elastic Net希望得到的自变量系数是在由t控制的一个范围内。 这一约束也是Elastic Net模型能进行复杂度调整,LASSO回归能进行变量筛选和复杂度调整的原因。 我们可以通过下面的这张图来解释这个道理:
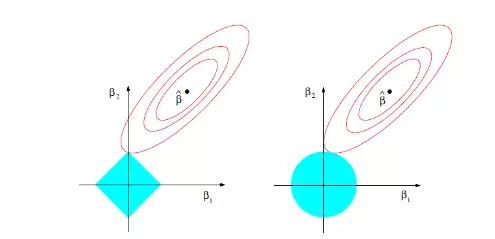
先看左图,假设一个二维模型对应的系数是β1和β2,然后是最小化误差平方和的点,即用传统线性回归得到的自变量系数。 但我们想让这个系数点必须落在蓝色的正方形内,所以就有了一系列围绕
的同心椭圆,其中最先与蓝色正方形接触的点,就是符合约束同时最小化误差平方和的点。 这个点就是同一个问题LASSO回归得到的自变量系数。 因为约束是一个正方形,所以除非相切,正方形与同心椭圆的接触点往往在正方形顶点上。而顶点又落在坐标轴上,这就意味着符合约束的自变量系数有一个值是0。 所以这里传统线性回归得到的是β1和β2都起作用的模型,而LASSO回归得到的是只有β2有作用的模型,这就是LASSO回归能筛选变量的原因。
而正方形的大小就决定了复杂度调整的程度。假设这个正方形极小,近似于一个点,那么LASSO回归得到的就是一个只有常量(intercept)而其他自变量系数都为0的模型,这是模型简化的极端情况。 由此我们可以明白,控制复杂度调整程度的λ值与约束大小t是呈反比的,即λ值越大对参数较多的线性模型的惩罚力度就越大,越容易得到一个简单的模型。
另外,我们之前提到的参数α就决定了这个约束的形状。刚才提到LASSO回归(α=1)的约束是一个正方形,所以更容易让约束后的系数点落在顶点上,从而起到变量筛选或者说降维的目的。 而Ridge回归(α=0)的约束是一个圆,与同心椭圆的相切点会在圆上的任何位置,所以Ridge回归并没有变量筛选的功能。 相应的,当几个自变量高度相关时,LASSO回归会倾向于选出其中的任意一个加入到筛选后的模型中,而Ridge回归则会把这一组自变量都挑选出来。 至于一般的Elastic Net模型(0<α<1),其约束的形状介于正方形与圆形之间,所以其特点就是在任意选出一个自变量或者一组自变量之间权衡。
回归方法的选择
- 岭回归:更加适合于变量之间具有高相关性,具有多重共线性的数据。
- LASSO:更加适用于高维数据,更能解决自变量大于样本量的数据情况。
- 岭回归 + LASSO回归 = 弹性网(ElasticNet)回归
- 最万能的方法是用LASSO, Ridge和Elastic Net都试试,比较三者Cross Validation的结果。
| α value | Model |
|---|---|
| 1 | LASSO回归 |
| 0 | Ridge回归 |
| 0<α<1 | Elastic Net模型 |
惩罚大小λ对模型拟合的影响
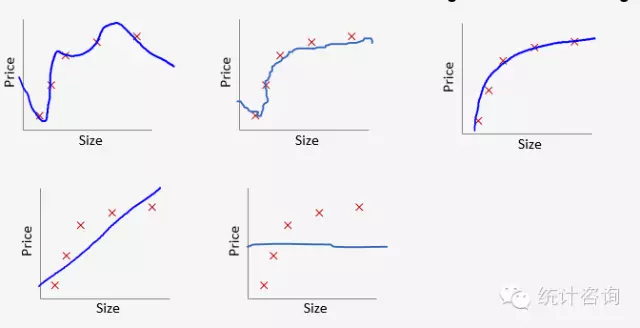
当λ取0时,也就是没有惩罚,为过拟合,拟合情况如上图1;当λ取无穷大时,系数都被压缩为0而只剩下θ0,为低拟合,拟合情况如上图5。λ从0到无穷大时,模型拟合是一个从过拟合到低拟合的过程。上图3为理想模型,怎样选择最优的λ得到理想模型呢?通过交叉验证方法(cross-validation)。
交叉验证选择最优λ
机器学习一般将样本集分为训练集(训练模型)、验证集(模型选择)、测试集(测试泛化能力)。
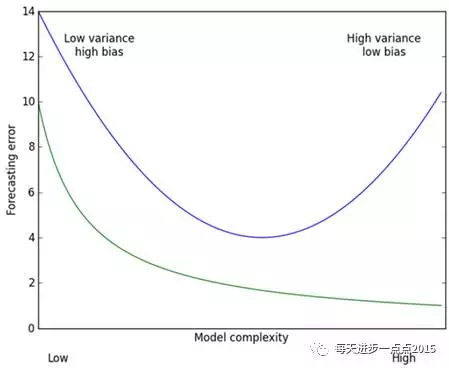
用图来解释,上图中横坐标是模型的复杂度,纵坐标是模型的预测误差,绿色曲线代表的是模型在训练集上的效果,蓝色曲线代表的是模型在测试集的效果。从预测效果的角度来看,随着模型复杂度的提升,在训练集上的预测效果会越来越好,呈现在绿色曲线上就是预测误差越来越低,但是模型运用到测试集的话,预测误差就会呈现蓝色曲线的变化,先降低后上升(过拟合);从模型方差(即回归系数的方差)来看,模型方差会随着复杂度的提升而提升。针对上面这个图而言,我们是希望平衡方差和偏差来选择一个比较理想的模型,对于岭回归来说,随着lambda的增大,模型方差会减小(因为矩阵X’X行列式在增大,其逆就是减小,从而使得岭回归系数在减小)而偏差会增大。故通过lambda来平衡模型的方差和偏差,最终得到比较理想的岭回归系数。LASSO回归复杂度调整的程度由参数λ来控制,λ越大对变量较多的线性模型的惩罚力度就越大,从而最终获得一个变量较少的模型。
选择交叉验证误差最小时候的λ值为模型最优值。
