目前最好用的拟合广义线性模型的R package是glmnet,由LASSO回归的发明人,斯坦福统计学家Trevor Hastie领衔开发。 它的特点是对一系列不同λ值进行拟合,每次拟合都用到上一个λ值拟合的结果,从而大大提高了运算效率。 此外它还包括了并行计算的功能,这样就能调动一台计算机的多个核或者多个计算机的运算网络,进一步缩短运算时间。
以Logistic回归为例, 了解如何使用glmnet拟合LASSO回归:
Data preparation
library(glmnet) #载入R包glmnet
df <- read.table("https://raw.githubusercontent.com/chenyuan-date/Data/master/LassoExample.txt", fill = T, header = T, sep = "\t") #读入试验用数据
Data pre-processing
在函数glmnet()中,不能使用类似y ~ x的公式,而是需要输入自变量x和因变量y。因此,在使用函数glmnet()前,需要先处理数据,准备好合适的x和y。
glmnet只能接受数值矩阵作为模型输入,如果自变量中有离散变量的话,需要把这一列离散变量转化为几列只含有0和1的向量,这个过程叫做One Hot Encoding。
library(caret)
set.seed(1024)
# 根据y随机切分为训练集和测试集,其中75%的数据用于训练模型,剩下的25%的数据用于测试。
train_index <- createDataPartition(y=df$y, p=0.75, list=FALSE)
#each group has the same proportion
train <- df[train_index,]
test <- df[-train_index,]
# glmnet输入参数为matrix,所以需要先将数据转为矩阵
train_matrix <- as.matrix(train[, -1])
test_matrix <- as.matrix(test[, -1])
Run lasso
函数cv.glmnet()可以实现CV选择合适的lambda
cvfit = cv.glmnet(train_matrix, train$y, family = "binomial", type.measure = "class", nfolds = 10, alpha = 1)
- 参数family规定了回归模型的类型:
- family=”gaussian”适用于一维连续因变量(univariate)
- family=”mgaussian”适用于多维连续因变量(multivariate)
- family=”poisson”适用于非负次数因变量(count)
- family=”binomial”适用于二元离散因变量(binary)
- family=”multinomial”适用于多元离散因变量(category)
-
参数lambda的值可以手动设置,不过函数glmnet()可以自动的给一个比较合适的lambda的向量,该向量的长度默认是100。
-
type.measure用来指定交叉验证选取模型时希望最小化的目标参量,对于Logistic回归有以下几种选择:
-
type.measure=deviance 使用deviance,即-2倍的Log-likelihood (default)
-
type.measure=mse 使用拟合因变量与实际应变量的mean squred error
-
type.measure=mae 使用mean absolute error
-
type.measure=class 使用模型分类的错误率(missclassification error)
-
type.measure=auc 使用area under the ROC curve,是现在最流行的综合考量模型性能的一种参数
-
nfolds设置把数据均分的份数,默认为10。或者用foldid指定每个fold的内容, 因为每个fold间的计算是独立的
-
parallel=TRUE可以开启并行计算功能来提高运算效率,需要先装载doParallel包。
-
参数alpha控制选择的模型类型:当alpha = 0, 用ridge回归;当alpha = 1, 用lasso回归。
绘制交叉验证图
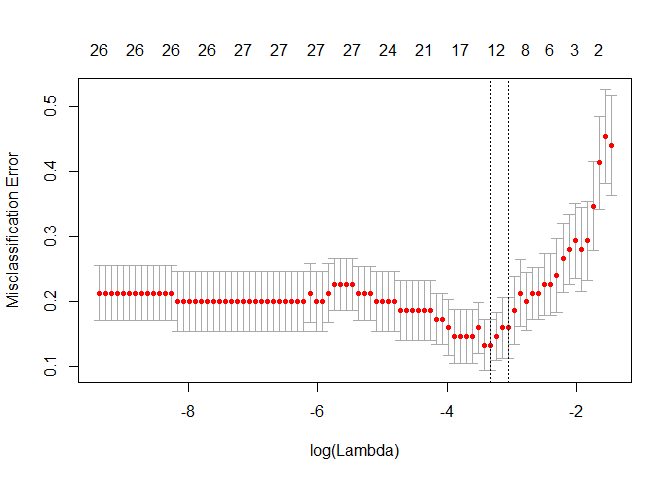
选择交叉验证误差最小时候的λ值为模型最优值。
函数plot()可以画出以log(lambda)为横坐标,以CV值为纵坐标的散点图。
plot(cvfit)
函数coef()可以得到最小的CV值所对应的系数的估计值。注意,在这里,需要设置参数s=”lambda.min”。
coef(cvfit, s = "lambda.min")[1:20, ]
## (Intercept) X1 X2 X3 X4
## 0.209032414 0.019470850 0.456609757 -0.022029524 -0.545612745
## X5 X6 X7 X8 X9
## -0.294964969 -0.763898848 0.000000000 -0.070116535 0.220941211
## X10 X11 X12 X13 X14
## -1.140961395 0.000000000 -0.009436584 0.000000000 0.000000000
## X15 X16 X17 X18 X19
## 0.000000000 0.022926030 0.000000000 0.000000000 0.000000000
因为交叉验证,对于每一个λ值,在红点所示目标参量的均值左右,我们可以得到一个目标参量的置信区间。 两条虚线分别指示了两个特殊的λ值:
c(cvfit$lambda.min, cvfit$lambda.1se)
## [1] 0.03590752 0.04746763
lambda.min表示测试误差最小时所对应的λ值
lambda.1se指在lambda.min一个方差范围内得到最简单模型的那一个λ值。因为λ值到达一定大小之后,继续增加模型自变量个数即缩小λ值,并不能很显著的提高模型性能,lambda.1se给出的就是一个具备优良性能但是自变量个数最少的模型。
指定λ值进行预测
pred.lasso <- predict(cvfit, test_matrix, type="response", s="lambda.1se")
这里的type有以下几种选择:
- type=link 给出线性预测值,即进行Logit变换之前的值
- type=response 给出概率预测值,即进行Logit变换之后的值
- type=class 给出0/1预测值
- type=coefficients 罗列出给定λ值时的模型系数
- type=coefficients 罗列出给定λ值时,不为零模型系数的下标
回归系数图
plot(cvfit$glmnet.fit,xvar ="lambda", label = T)
abline(v=log(c(cvfit$lambda.min,cvfit$lambda.1se)),lty=2)
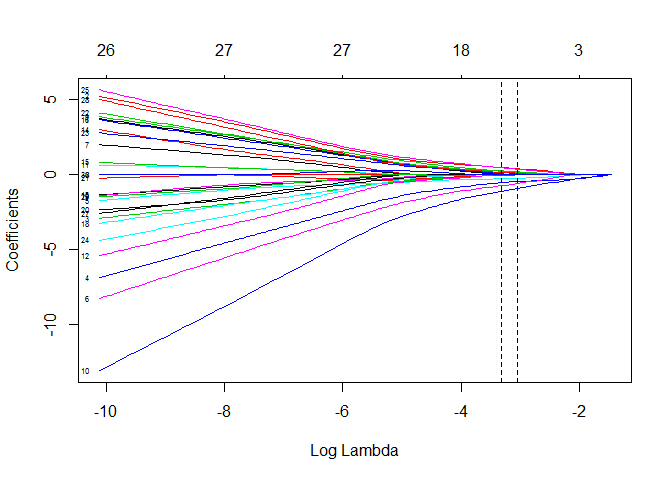
- xvar = lambda表示横坐标是log(lambda)
- label = T表示标示出图左边的自变量的名称
每条彩色线是模型中的每个变量,随着λ增加,每个变量的系数会变小,在λ最优时候,有些变量的系数被精准地压缩为0,从而保留了系数不为0的变量,实现了变量选择。
回归方法的选择
最万能的方法是用LASSO, Ridge和Elastic Net都试试,比较三者Cross Validation的结果。
# CV for 11 alpha value
y <- df$y
x <- model.matrix(y ~., df)[, -1]
for (i in 0:10) {
assign(paste("cvfit", i, sep=""),
cv.glmnet(x, y, family="binomial", type.measure="class", alpha=i/10))
}
# Plot Solution Paths
par(mfrow=c(3,1))
plot(cvfit10, main="LASSO")
plot(cvfit0, main="Ridge")
plot(cvfit5, main="Elastic Net")
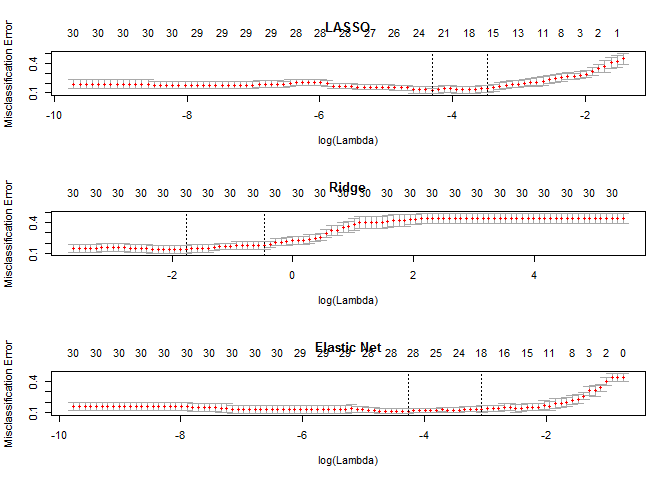 通过比较可以看出,Ridge回归得到的模型一直都有30个自变量,而α=0.5时的Elastic Net与LASSO回归有相似的性能。
通过比较可以看出,Ridge回归得到的模型一直都有30个自变量,而α=0.5时的Elastic Net与LASSO回归有相似的性能。
